لكل حبيباتي في الجامعة او الكلية او المعاهد انا متخصصة في تدريس مادة الرياضيات لمن احبت ان تراسلني على الخاص
حتى لو حلول اسئلة واجبات ...
حياكن الله
حتى لو حلول اسئلة واجبات ...
حياكن الله
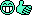
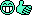








 يسمى المميز .
يسمى المميز . 




 - ك **
- ك ** - ك يكافئ
- ك يكافئ - ك )
- ك )  - ك )
- ك ) -3ك2
-3ك2  بالتكعيب
بالتكعيب


 (2)
(2)


تعليق